不同的二叉搜索树

题目

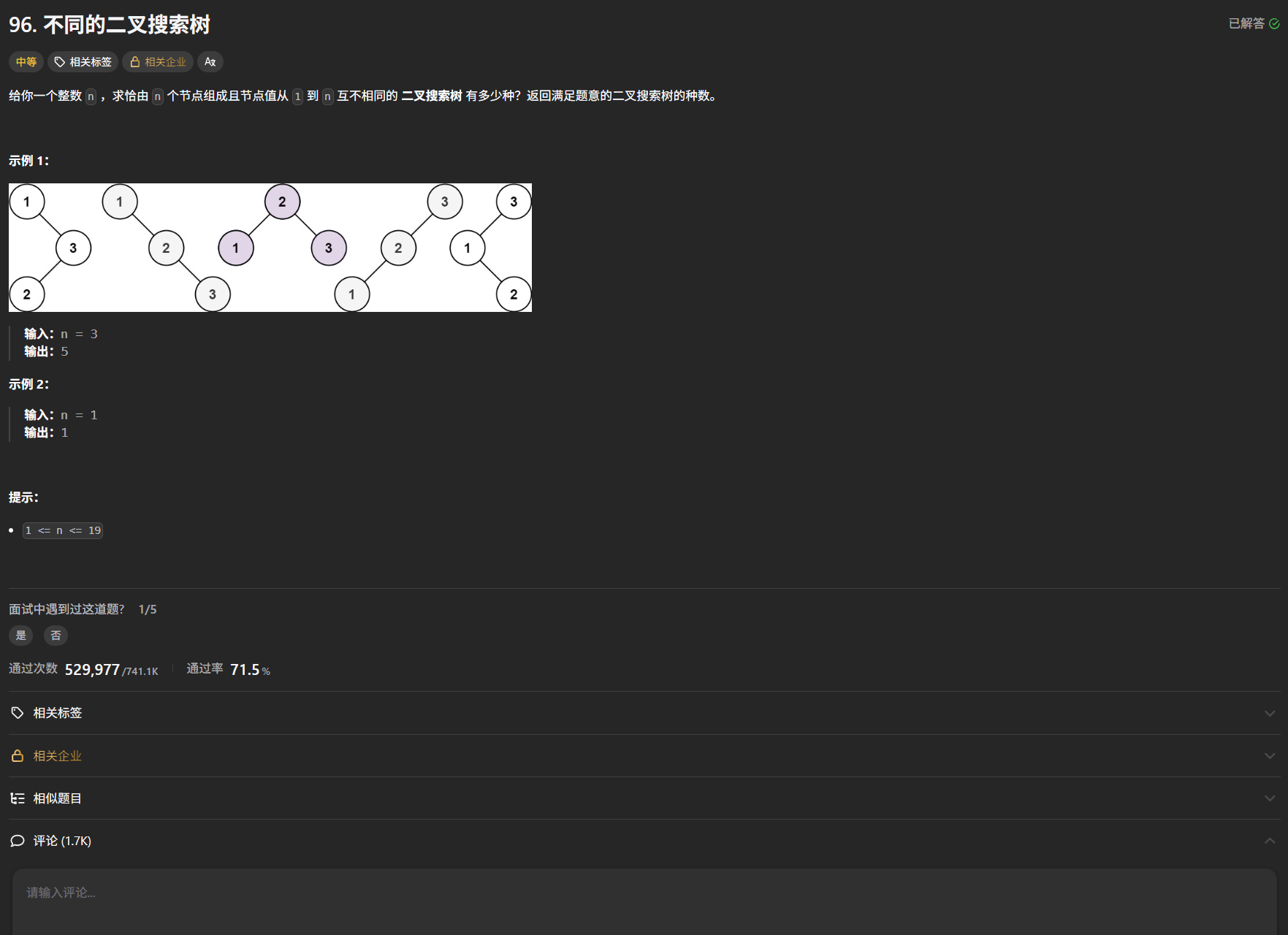
首先这是一棵二叉搜索树，是有顺序的，所以考虑 1 − n 的顺序的话，就完整的确定了一棵二叉搜索树。

具体思路

1. 从 1 − n 轮流作为根节点，分别确定左右两棵子树的左右子树的位置
2. 以某个 i为根节点的个数 = 其左子树存在的个数 * 右子树存在可能的个数（其实我们应该能想到，当固定某一整个大的部分不变时，讨论某个小部分不变的话，就可以找到所有的子树。
3. 最终总的个数的话，就是每一个根节点的可能相加了。然后在计算左右子树的同时是要用到前面所有的可能，所以我们不能压缩数组）。

具体实现

class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 1;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i] += dp[i - j] * dp[j - 1];
            }
        }
        return dp[n];
    }
}

如何将这个问题划分为若干个子问题？

class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n + 1, 0);
        dp[0] = 1;

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i] += dp[i - j] * dp[j - 1];
            }
        }

        return dp[n];
    }
};