最小花费爬楼梯

题目

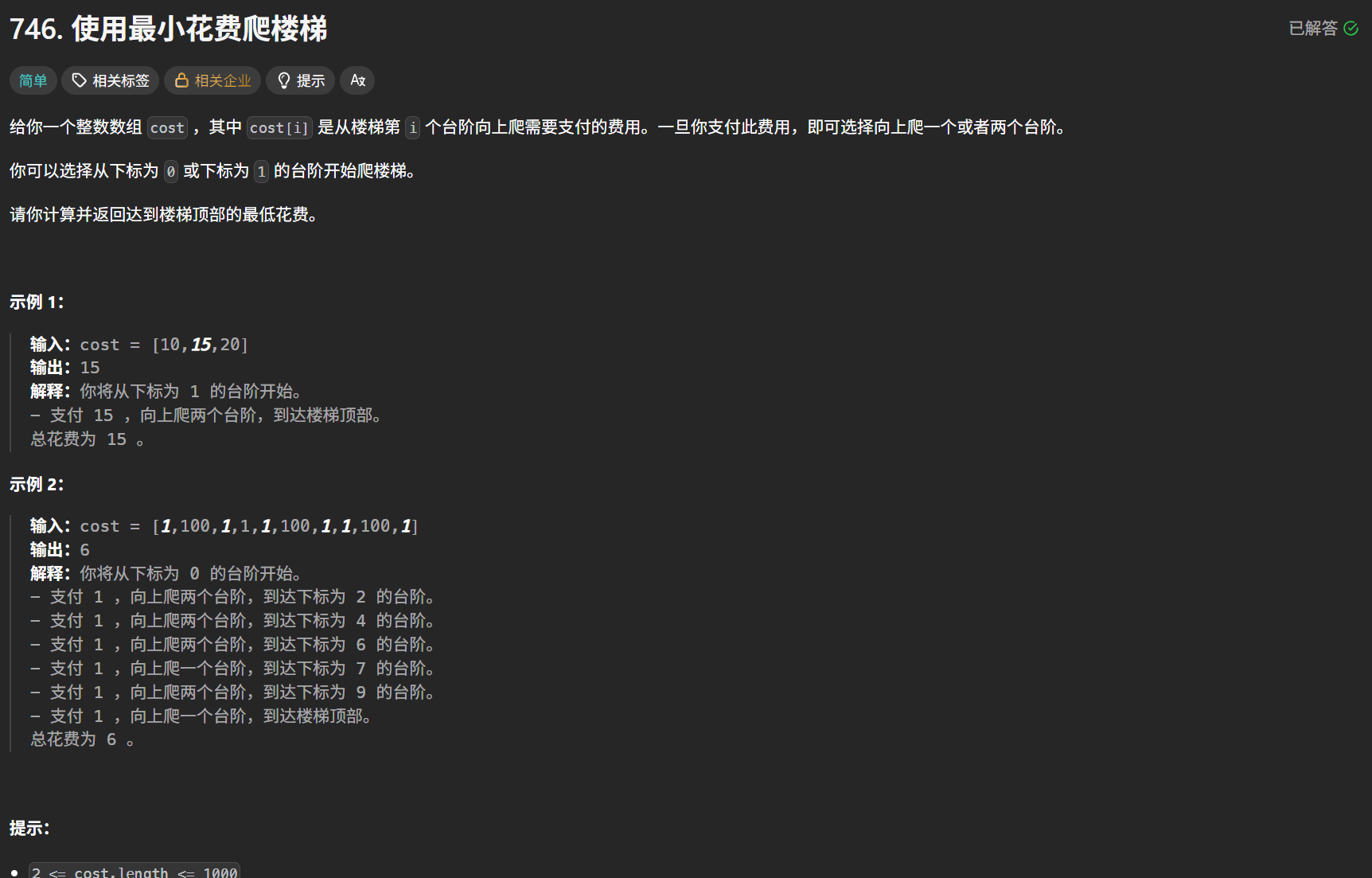
根据 cost.length ，我们不需要考虑特殊情况。

题目的意思在于爬到 c o s t . l e n g t h 的位置，需要花费多少，仅仅是爬到 c o s t . l e n g t h − 1 是不能直接到达终点的，还需要花费该位置的 数字 。

具体思路

1. 最后一位的花费取决于 Math.min(cost[i - 2] + res[i - 2] , cost[i - 1] + res[i - 1] )之中最小的花费。
2. 因此计算最后一位的过程中，还是需要计算前面所有的花费。那么也就是分为保存中间结果和不保存中间结果两种情况。

具体实现

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int[] res = new int[cost.length + 2];
        // cost = [1,100,1,1,1,100,1,1,100,1]
        // 0 0 1 2 2 3 3 4 4 5 6
        for (int i = 2; i <= cost.length; i++) {
            res[i] = Math.min(res[i - 1] + cost[i - 1], res[i - 2] + cost[i - 2]);
        }
        return res[cost.length];
    }
}

这里我们保存中间的结果，最后返回结果即可。

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int pre = 0;
        int next = 0;
        int res = -1;
        for (int i = 2; i <= cost.length; i++) {
            res = Math.min(pre + cost[i - 2], next + cost[i - 1]);
            pre = next;
            next = res;
        }
        return res;
    }
}

类似于斐波那契数列，这里我们使用两个变量来动态滑动数组的中间结果，减少空间复杂度。

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        vector<int> dp(cost.size() + 1, 0);
        if (cost.size() < 2) {
            return 0;
        }

        dp[0] = 0;
        dp[1] = 0;

        for (int i = 2; i <= cost.size(); i++) {
            dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
        return dp[cost.size()];
    }
};