目标和

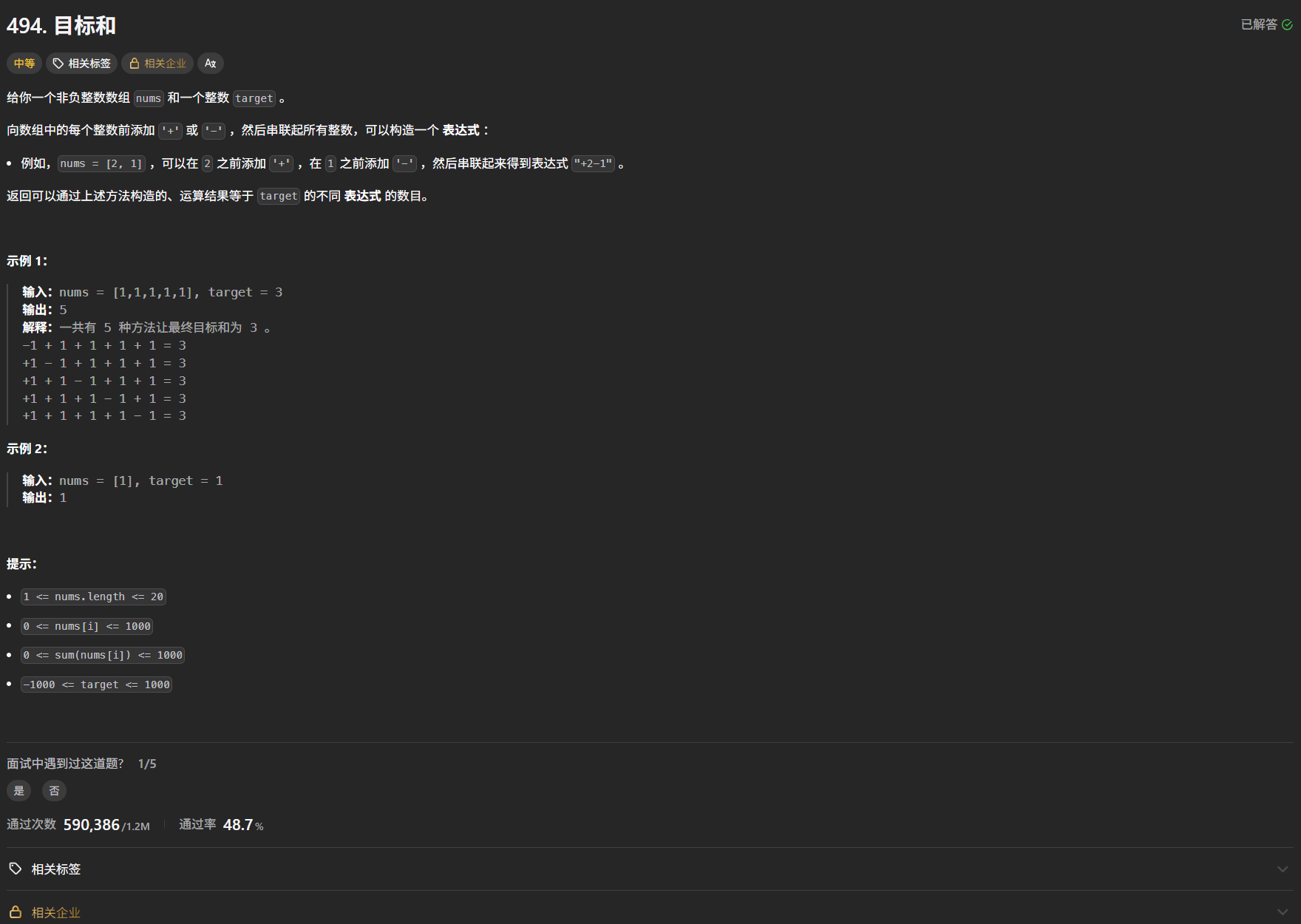
题目

具体思路

1. 类似于[[14. 最后一块石头的重量Ⅱ]]，不同的是，这里的是需要计算粉碎石头的个数。
2. 背包的容量也是在保留的基础上计算剩下的 石头 能不能分成两块，如果可以分成两块那么可以计算，否则直接整除的话，会让分不成的 石头 多余一块。
3. 计算有多少种组合方式：将 dp[n] 转换成组合当前的个数有多少种方式，那么需要初始化一个 dp[0] = 1 ,然后每遍历到一件物品增加当前的个数。

具体实现

class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        int total = 0;
        for (int i = 0; i < nums.length; i++) {
            total += nums[i];
        }
        if ((total - target) % 2 == 1 || Math.abs(target) > total) {
            return 0;
        }
        int space = target + (total - target) / 2;

        int[] dp = new int[space + 1]; // 当前space容量有多少种的组合
        dp[0] = 1;
        int res = 0;
        for (int i = 0; i < nums.length; i++) {
            for (int j = space; j >= nums[i]; j--) {
                dp[j] += dp[j - nums[i]]; //当前这种负数选定了，然后直接加上减去的总的个数
            }
        }
        return dp[space];
    }
}

这里的状态转移方程比较不太一样。然后我们怎么将背包的存储问题转换成装满背包的个数问题。

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        int sum = 0;
        for (int i = 0; i < nums.size(); i++) {
            sum += nums[i];
        }
        if (abs(sum) < abs(target))
            return 0;
        if ((target + sum) % 2 == 1) {
            return 0;
        }
        int space = (target + sum) / 2;

        vector<int> dp(space + 1, 0);
        dp[0] = 1;
        for (int i = 0; i < nums.size(); i++) {
            for (int j = space; j >= nums[i]; j--) {
                dp[j] += dp[j - nums[i]];
            }
        }
        return dp[space];
    }
};