一和零

题目

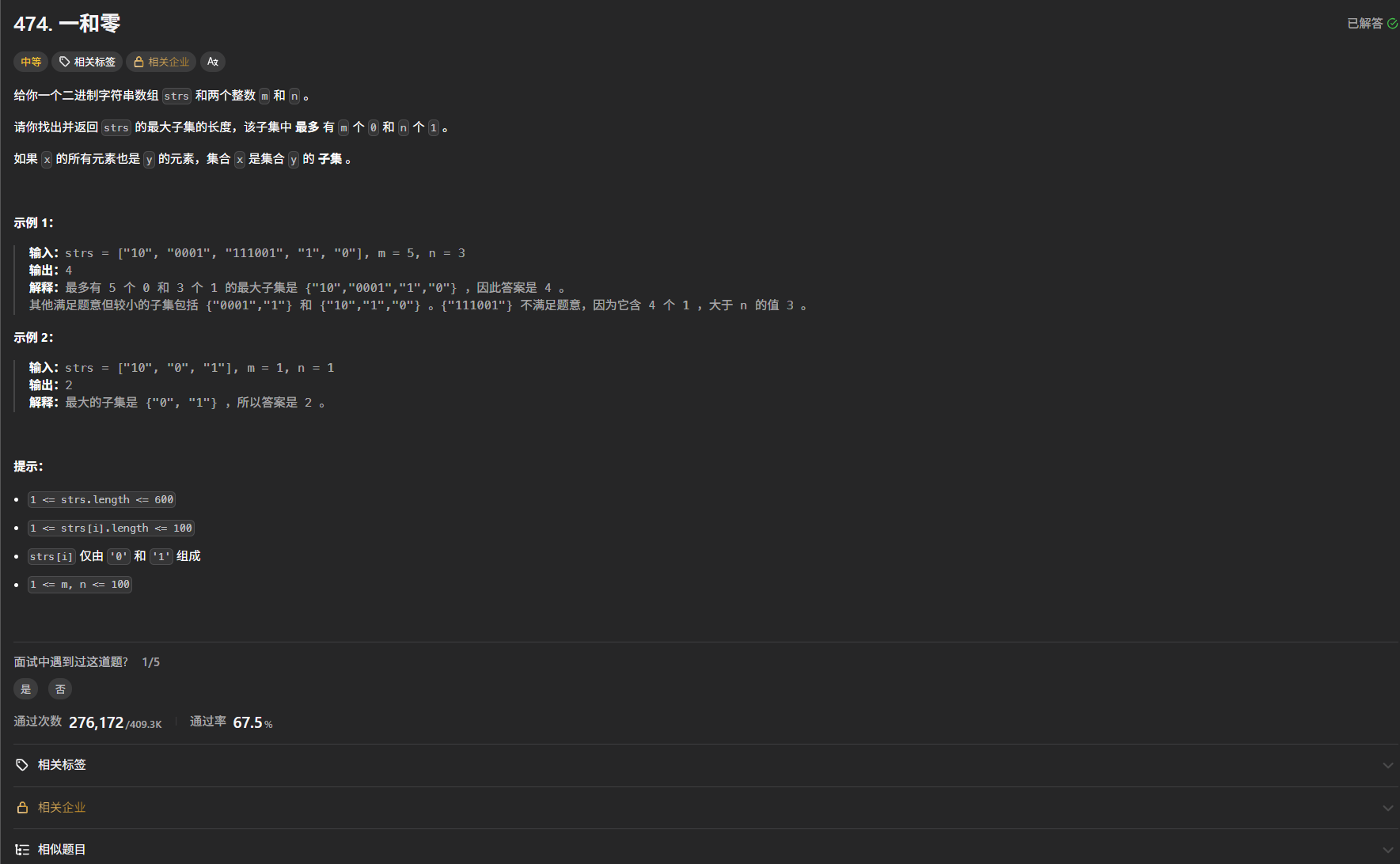
具体思路

1. 我们要记录下一个 str 的 zeroNum 和 oneNum 的个数，所以呢我们可以定义一个内部类，但是也可以不用定义直接将处理的过程添加到计算 str 的内层循环中；
2. 类似于[[16. 目标和]]， 我们这里需要装满的是 m 和 n 两个东西，那么就是需要定义一个三维数组（另一个维度是轮数），但是我们从后向前遍历的话可以省去这一个步骤；
3. 最后我们确定中间的转移方程：计算的当前的最大长度，那么我们需要判断当前长度和添加物品之后的哪个更长 —> dp[j][k] = Math.max(dp[j][k], dp[j - array[i].zeroNum][k - array[i].oneNum] + 1);

具体实现

class Solution {
    class ty {
        int zeroNum;
        int oneNum;

        public ty(int zeroNum, int oneNum) {
            this.zeroNum = zeroNum;
            this.oneNum = oneNum;
        }
    }

    public int findMaxForm(String[] strs, int m, int n) {
        ty[] array = new ty[strs.length];
        for (int i = 0; i < strs.length; i++) {
            int zeroNum = 0;
            int oneNum = 0;
            for (int j = 0; j < strs[i].length(); j++) {
                if (strs[i].charAt(j) == '0') {
                    zeroNum++;
                } else {
                    oneNum++;
                }
            }
            array[i] = new ty(zeroNum, oneNum);
        }

        int[][] dp = new int[m + 1][n + 1];
        for (int i = 0; i < strs.length; i++) {
            for (int j = m; array[i].zeroNum <= j; j--) {
                for (int k = n; array[i].oneNum <= k; k--) {
                    dp[j][k] = Math.max(dp[j][k], dp[j - array[i].zeroNum][k - array[i].oneNum] + 1);
                }
            }
        }
        return dp[m][n];
    }
}

状态转移方程还是有问题

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        int targetZero = m, targetOne = n;

        vector<pair<int, int>> num;
        for (int i = 0; i < strs.size(); i++) {
            int temp0 = 0, temp1 = 0;
            int j = 0;
            while (j < strs[i].size()) {
                if (strs[i][j] == '1') {
                    temp1++;
                } else {
                    temp0++;
                }
                j++;
            }
            num.push_back({temp0, temp1});
        }

        vector<vector<int>> dp(targetZero + 1, vector<int>(targetOne + 1, 0));
        for (int i = 0; i < strs.size(); i++) {
            for (int j = targetZero; j >= num[i].first; j--) {
                for (int t = targetOne; t >= num[i].second; t--) {
                    dp[j][t] = max(dp[j][t],
                                   dp[j - num[i].first][t - num[i].second] + 1);
                }
            }
        }

        return dp[targetZero][targetOne];
    }
};